EPJ E Highlight - Modelling microswimmers for drug delivery
- Details
- Published on 11 November 2020
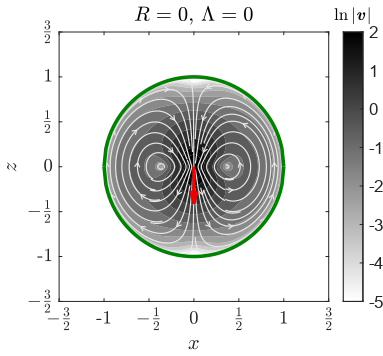
Mathematical models of the motion of cells in viscous liquids that show how this motion is affected by the presence of a surfactant coating have applications in the design of artificial microswimmers for targeted drug delivery, micro-surgery and other applications.
Many types of motile cells, such as the bacteria in our guts and spermatozoa in the female reproductive tracts, need to propel themselves through confined spaces filled with viscous liquid. In recent years, the motion of these ‘microswimmers’ has been mimicked in the design of self-propelled micro- and nano-scale machines for applications including targeted drug delivery. Optimising the design of these machines requires a detailed, mathematical understanding of microswimmers in these environments. A large, international group of physicists led by Abdallah Daddi-Moussa-Ider of Heinrich-Heine-Universität Düsseldorf, Germany has now generated mathematical models of microswimmers in clean and surfactant-covered viscous drops, showing that the surfactant significantly alters the swimmers’ behaviour. They have published their work in EPJ E.
The dynamics of microswimmers moving inside a drop of viscous liquid depends on many things, including the shape and size of the drop, the number of microswimmers and the Reynolds number of the liquid. This is a measure of viscosity; liquids with low Reynolds number are more viscous and flow in a linear manner with little turbulence. The flow of such a liquid can be modelled by solving a set of partial differential equations known as the Navier-Stokes equations. In this case, the microswimmer itself was considered as a force dipole confined within the drop and located at a set point. The presence of a layer of surfactant surrounding the drop containing the microswimmer was modelled using boundary conditions.
Solving these equations in a range of conditions – drops with or without surfactant coats, stationary and freely moving, and with different Reynolds numbers and radii – gave Daddi-Moussa-Ider and his co-workers a set of subtly different flow fields, from which the dynamics of the microswimmer could be defined. They note that these models of swimmer dynamics may prove useful in designing micro-machines for materials assembly, biosensing and micro-surgery as well as drug delivery.
A.R. Sprenger, V.A. Shaik, A.M. Ardekani, M. Lisicki, A.J.T.M. Mathijssen, F. Guzmán-Lastra, H. Löwen, A.M. Menzel, and A. Daddi-Moussa-Ider (2020), Towards an analytical description of active microswimmers in clean and in surfactant-covered drops, Eur. Phys. J. E 43:58. https://doi.org/10.1140/epje/i2020-11980-9





